本文译自《SAE International Journal of Vehicle Dynamics, Stability, and NVH》
收录文章《Robust Control of a Four-Wheel-Independent-Steering Electric Vehicle for Path Tracking》
原作者：同济大学智能汽车研究所杭鹏博士，陈辛波教授及罗凤梅硕士
摘要 ：与传统的前轮转向汽车相比，四轮独立转向汽车有更好的操纵稳定性和路径跟踪能力。鉴于此，本文提出了一种新型的带有线控转向系统的四轮独立转向电动汽车。对于四轮独立转向电动汽车，考虑到车辆参数不确定性的影响，设计了一种利用μ综合方法的鲁棒控制器，并基于Hankel范数近似实现了控制器降阶。为了评估所设计的控制器的性能，使用具有9个自由度(DOF)的非线性车辆模型在MATLAB / Simulink中进行了两种策略的数值模拟。仿真结果表明，鲁棒控制器在名义车辆模型方面的跟踪精度优于LQR最优控制器。此外，鲁棒控制器可以使车辆在不同车速和道路摩擦系数的情况下很好地跟踪目标路径，这表明鲁棒控制器具有较强的稳定鲁棒性和较好的抗参数摄动的性能鲁棒性。
1前言
近年来，自动驾驶技术已成为智能交通系统中用来减少交通问题的新兴研究热点。路径跟踪是自主地面车辆(AGV)的基本功能和主要任务。设计的路径跟踪控制器被要求能够使车辆以较小的跟踪误差跟踪目标路径，包括侧向偏移和航向误差。
与前轮转向车辆相比，四轮转向车辆具有出色的机动性，操纵稳定性和路径追踪能力，因此它更适合被作为自主地面车辆(AGV)使用。由于四轮转向车辆的路径跟踪问题比前轮转向车辆的路径跟踪问题更复杂，因此目前四轮转向车辆的路径跟踪控制策略仍然相对有限。
本文提出了一种新型的带有线控转向系统的四轮独立转向电动汽车，并设计了用于路径跟踪的控制器。通过MATLAB / Simulink数值仿真比较所设计的μ综合+ 4WIS + DYC与LQR + 4WIS + DYC两种路径跟踪控制器性能。目的是设计一种先进的控制器，以改善路径跟踪能力，并获得良好的抗参数摄动和外部干扰的鲁棒性。
2四轮独立转向电动车构型
本团队提出并制造了一种新型的4WIS（四轮独立转向）电动车，如图1所示。为了实现四轮独立转向，4WIS电动汽车由四个SBW（线控转向）系统组成。从图2可以看出，SBW系统是转向系统和悬架系统的集成设计，主要由转向电机、蜗杆减速器、减震器、转向盘转角传感器等组成。车轮可通过减速器、上滑动柱、上摆动臂、下摆动臂和下滑动柱围绕由所述转向电机驱动的主销旋转。利用方向盘转角传感器实时测量各轮的转向角信号，进行路径跟踪控制。表1显示了4WIS EV的结构参数。
图1 4WIS EV
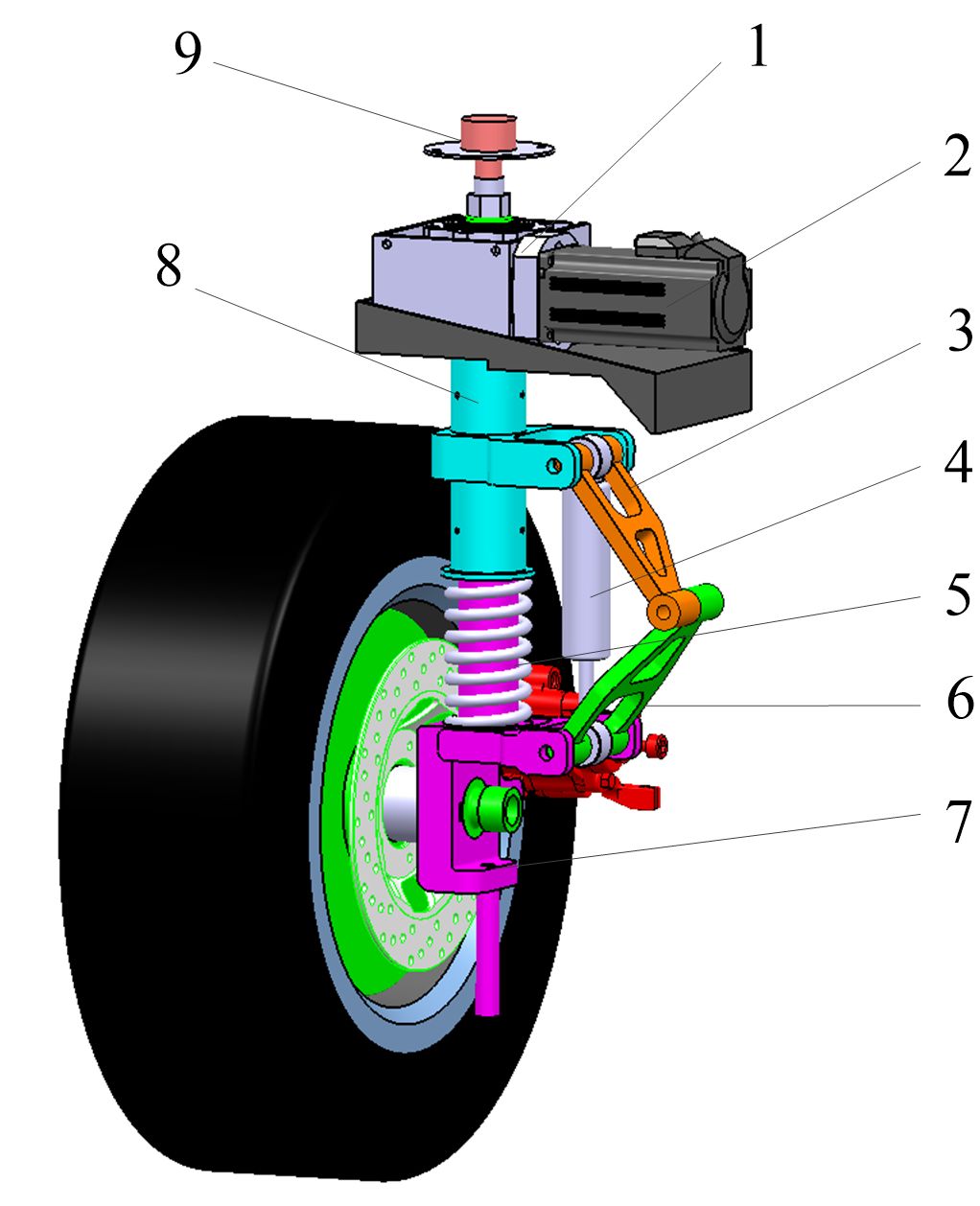
图2 SBW系统：1，蜗杆和齿轮减速器；2，转向马达；3，上摆动臂；4，减震器；5，弹簧；6，下摆动臂；7，下滑动柱；8，上滑动柱；9，车轮转向角传感器
表1 4WIS EV的结构参数
3建模
四轮独立转向电动汽车动力学模型
在这一部分中，将4WIS EV的动力学模型简化为2自由度的单轨模型。如图3所示，只考虑侧向和横摆运动，以尽量减少建模的复杂性，假设纵向速度为u，单轨模型有三个输入：前转向角δf、后转向角δr和附加横摆力矩ΔMz。单轨模型的非线性动力学方程如下：
其中v是车辆的侧向速度，r是车辆的横摆角速度，Fyf和Fyr分别是前后的侧向轮胎力。
在控制器设计中，假设轮胎滑移角很小，轮胎力与轮胎滑移角成线性关系，于是有：
将上述两个方程的后者带入前者，则信号轨迹模型的动力学方程可表示为：
路径跟踪
图3为4WIS EV的路径跟踪模型。xy为车身坐标系，xdyd坐标系表示其目标路径上的车辆方向。
图3 4WIS EV路径跟踪动力学模型
在本文中，路径跟踪问题等价于最小化侧向位置误差和横摆角误差，这两个误差可以表示为：
取一个关于时间的导数，上述方程可以重写为：
ρ为目标路径的曲率半径。
侧向位置误差的导数推导如下：
结合前面几个方程，4WIS电动汽车路径跟踪的动力学方程可以写成状态空间形式：
状态向量
，控制输入向量
和外部输入向量
，系数矩阵A，B，C，D和E由下给出：
4鲁棒控制
在路径跟踪过程中，车辆速度和轮胎侧偏刚度等参数不能始终保持不变。此外，侧风、变径曲率等外部扰动也是不可避免的。结果表明，4WIS EV的路径跟踪性能严重恶化.因此，有必要设计一种对参数扰动和外部扰动具有良好鲁棒性的控制器。在此基础上，设计了一种基于μ综合方法的鲁棒控制器。
鲁棒控制闭环系统
用于路径跟踪的4WIS EV鲁棒控制闭环系统如图4所示。该系统主要由G模型、控制器K和其他性能对象元素组成。
图4 用于路径跟踪的4WIS EV鲁棒闭环系统
模型 G 是一个摄动模型结合标准模型Gnorm不确定块Δ。G可以以上线性分式变换(LFT)的形式表示为
。不确定块Δ反映了速度和轮胎侧偏刚度的参数不确定性，是一个对角矩阵且范数有界
， 闭环系统具有三个输入：路径信息W、外部干扰d和测量噪声n。输出eU和eY用于评价闭环系统的鲁棒性。加权函数WU和WP反映了U和 Y的性能输出, 权重函数Wn反映了不同频域对测量噪声的影响n。为了达到预期的鲁棒性能，选择了适当的加权函数，并将它们表示如下：
μ综合与D-K迭代
在图5中，P(s)表示由名义模型和加权函数组成的19个输入和17个输出开环系统的传递函数矩阵。用于路径跟踪的4WIS EV的广义系统如图6所示。
图5 用于路径跟踪的4WIS EV鲁棒控制开环系统
图6 用于路径跟踪的4WIS EV广义系统
对于鲁棒性能分析，不确定的块ΔP结构定义为：
第一个不确定块Δ用来描述参数扰动，第二个不确定块是一个虚拟的不确定性块ΔP，它是利用μ综合方法来表示鲁棒性能要求的。块ΔP的输入是eU和eY,块ΔP的输出是d，n和W。
为了达到鲁棒的性能要求，需寻找一个稳定控制器K(S)，使结构奇异值对于每个频率满足以下条件：
其中FL(P,K)是P和K的下线性分式变换，为了解决上述方程中的问题，采用了D-K迭代法。考虑到：
其中DΔP是任何一个满
，
且遵循DΔP=ΔPD的矩阵集。
500 Servlet Exception
[show] java.lang.IllegalStateException: sendError() forbidden after buffer has
been committed.
Resin/3.1.10
)