
在介绍两类指数之前,先简单介绍一下数据的类型。
计数型数据(又被称为离散型数据或属性型数据)
通常表示事物的分类,例如:
合格/不合格
产品A/产品B/产品C
一等品/二等品/三等品
极不满意/不满意/一般/满意/极满意
计量型数据 (又被称为连续型数据)
通常是通过测量仪器测量得到的数据,例如:
电池的寿命
零件的长度
孔的直径
产品的重量
热处理的温度
注塑的压力
通常,我们只考虑计算计量型的数据的过程能力。对于计数性数据(例如,合格率或不良率)虽然可以转化为西格玛水平Z,但是实际意义不大。大部分质量人员还是需要查表,才能从根据西格玛水平得出不良率,直接给出不良率更直观。
下面介绍一下过程能力指数Cp/Cpk和过程性能指数Pp/Ppk的区别。
计算过程能力指数Cp/Cpk,需要满足以下几个前提:
测量系统满足要求:MSA必须满足要求,如不满足要求,需要先改进测量系统。
数据来自稳定受控的过程:先要做基于过程控制的休哈特控制图(均值—极差图,单值—移动极差图……),如控制图存在判异情况,需要先消除特殊原因导致的变异。
数据正态分布:通常需要基于控制图的全部数据点的集合服从正态分布,至少也要保证均值图的数据和每个子组的数据集合服从正态分布。
数据相互独立:数据是随机抽取的,并且没有可预测性。
计算过程性能指数Pp/Ppk,需要满足以下几个前提:
测量系统满足要求:MSA必须满足要求,如不满足要求,需要先改进测量系统。
数据相互独立:数据是随机抽取的,并且没有可预测性。
从上面的描述可以发现,Cp/Cpk比Pp/Ppk多了两个前提要求。
1. 先要做过程控制图,过程稳定了才能计算Cp/Cpk。
2. 要求数据正态,不正态的数据不能计算Cp/Cpk。
此外,两个系列的差异在于对总体标准差的估计公式。
对于Cp/Cpk,计算组内标准差

需要按照一定的抽样间隔时间进行抽样,每个抽样间隔就是一个子组。
在控制图稳定的前提下,计算每个子组的极差。
计算平均极差,最后用为总体标准差的估计(基于正态前提)。
对于Pp/Ppk,计算整体标准差
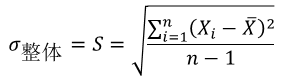
不需要按照抽样间隔时间进行抽样(允许连续抽样),当然按照抽样间隔抽样也可以。
不做控制图,数据不分子组,把所有数据合并成一个大组。
计算这个大组的整体标准差作为总体标准差的估计(基于正态前提),如果非正态,采用分位数方法。
过程能力指数和过程性能指数计算公式如下(基于正态分布)

特别强调,计算过程能力指数应该遵循以下步骤:
1. 先进行测量系统分析
2. 进行控制图判稳,如不满足稳定性前提,应分析原因并设法加以改善。
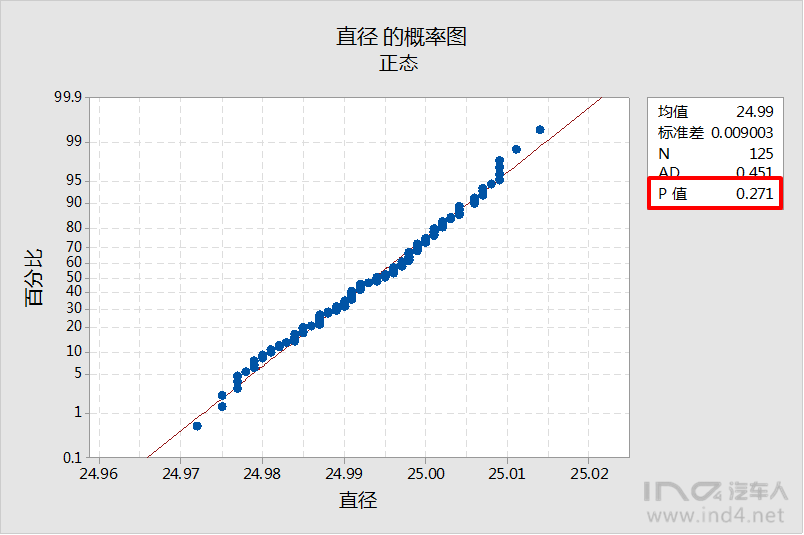
3. 进行正态性检验,如不满足正态性前提,应分析数据产生的机理是否正态,如果数据产生机理不应该是正态,应考虑对数据进行变换。
4. 进行独立性检验,连续性生产或是化工行业要特别注意独立性问题,独立性检验方法这里不做展开
完成以上工作后,才能进行过程能力指数计算,这里以Minitab为例:
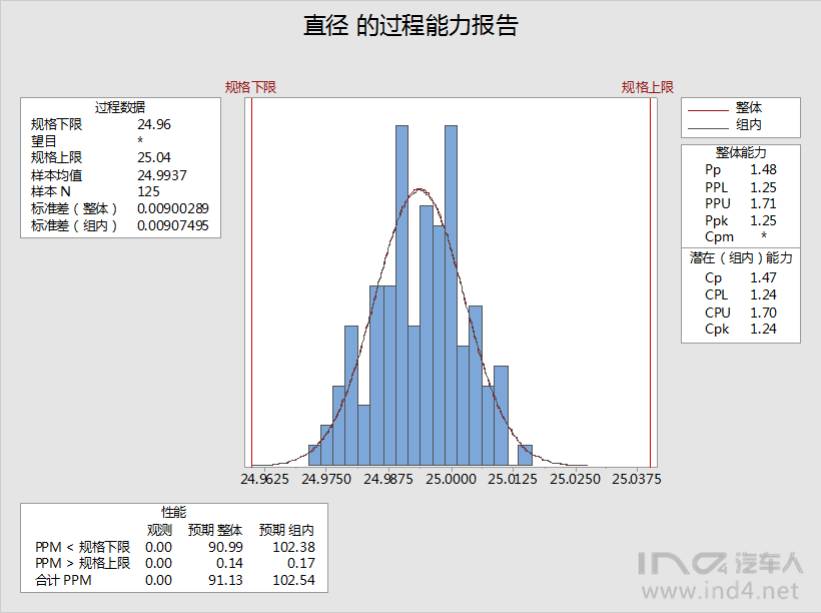
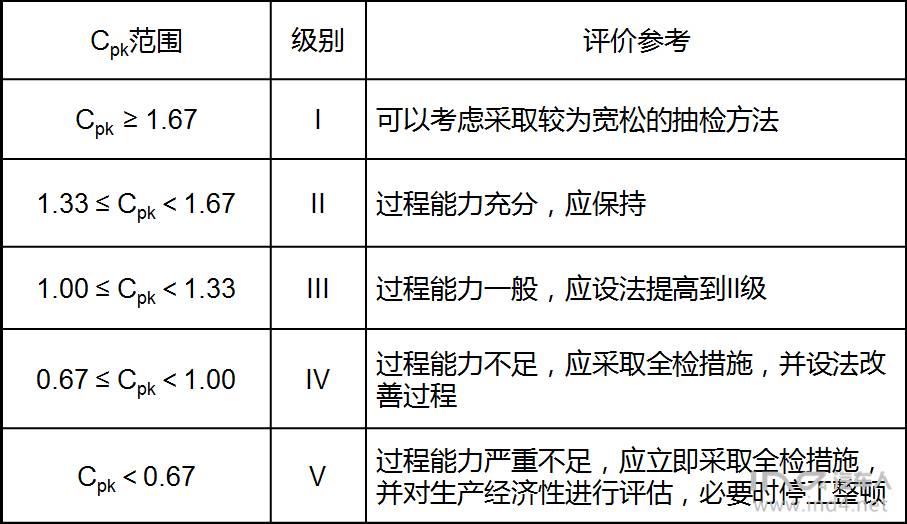
过程能力指数的要求如下:
新课上线
投产Launch